Blackjack is the most likely winning game in the casino and the only relatively fair game there, with players winning 49% of the time with the best play. However, if you want to win money in the long run, this 2% disadvantage is also intolerable. High-end gamblers will use the method of changing bets or team battles to regain this disadvantage.
How to play at 21
Although there are often scenes of blackjack in various movies, it is only popular in casinos after all, and not many people have actually played it. Let us first introduce the gameplay of blackjack.
This game is divided into banker and two sides. Usually, the banker deals with 5 to 7 players who are fighting each other at the same time on a semi-circular card table. The player's goal is to make the sum of his cards greater than the dealer's, but if the sum exceeds 21, he will be out of the game (that is, burst). Flowers count as 10 points, Aces can be counted as 11 points or 1 point as needed.
In the first round, both the player and the dealer will receive two initial cards, each of which will only be turned over. Each subsequent round, the player can choose:
- Take a card (Hit)
- End the card (Stand)
- Double the bet and take a card (Double)
- If the two cards are the same, the player can split the two cards, place another bet of the same, and get another two cards from the dealer, which is equivalent to playing two games at the same time (Split)
- admit defeat, surrender half and start the next round (Surrender)
It should be noted that Double, Split and Surrender can only be selected in the first round. Some casinos allow Double after Split or continue Split, while others do not allow Surrender.
When all players have finished taking cards, the dealer turns over the cards covered in the first round. If the sum of the points is less than 17, he will take the cards until the sum of the points is greater than or equal to 17. The dealer does not Double, Split or Surrender. If the dealer busts, all players win. If the dealer does not burst, the player with more points than the dealer wins.
Of course, there are also some special rules for blackjack such as Insurance and Blackjack (holding an ace and a 10), so I won't go into details here.
How high-end gamblers want their cards
You can see that blackjack is not complicated, and mathematicians can easily figure out the best card strategy. Calculations show that the best play allows players to win around 49% of the time. For professional gamblers, there is no difficulty in doing this. The so-called best play is just 3 matrices, and you can write them down.

The above 3 matrices cover almost all possible situations in the game. The top row of coordinates indicates the number of points the dealer has turned over in the first round (T is 10 points). The leftmost column of the first vertical row of the matrix represents the sum of the player's current hand card points, H is Hard, that is to say, the A in the hand card should be counted as 1 point (if any), and the leftmost column of the other two vertical rows Indicates what are the two cards in the player's hand.
The remaining matrix elements are the best actions for the player. Where H is Hit, S is Stand, P is Split, D is Double (Hit if the rules don't allow it), and Ds is Double (Stand if the rules don't allow it).
Looking closely at the 3 matrices above, many of the card strategies can be understood with a little thought. But there are also some interesting points, such as when the hand sum is 12, the dealer's hand is 2 or 3 to hit, 4 to 6 to stand, and when the dealer's hand is higher, it should be firmly held.
Why is this happening? When to ask for a card and when not to, the probability has the final say. Let's take a look at Stand's winrate at 12 o'clock. After the dealer starts to draw cards, the sum of points is greater than or equal to 17 until it stops. At this time, players can only hope that the dealer will bust their cards to win.
If the dealer's starting point is greater than or equal to 17, there is no draw at all. When the sum of the points is H16, it will explode when you draw 6~T. We know that the probability of drawing cards of different sizes is equal (1/13). Let F(x) be the probability of continuing to draw and bust when the current point sum is x, then:
F(H16) = 8/13 = 0.61538
When the banker's hand points sum to H15, draw 7~T and blow up; draw A, it will be reduced to H16:
F(H15) = 7/13 + 1/13×F(H16) = 0.58580
In the same way, the bust probability of H14 to H6 can be calculated. When the dealer's hand sum is H5, the situation is different. At this time, A can be counted as 11 points. After taking this change into account, it is not difficult to calculate the situation of H2-H5.
What if the player chooses Hit? There are two winning scenarios at this point:
The player didn't bust but the dealer busted
Neither the player nor the banker burst but the banker's points are small
The probability of busting has been calculated, and now consider the situation of the ratio. If the dealer's first card is a 2, let G(x) be the probability that the dealer will get a point and a hand of x, then G(H2) = 1.
If the dealer's hand sum becomes H3, he can only draw an ace in the case of H2, namely:
G(H3) = 1/13×G(H2) = 0.07692
Similarly, the probability of H4 to H21 can be calculated, still pay attention to the case where A is calculated as 11 points. In the case that neither side is busted, there are only the following possibilities for the player to win through the ratio:
The player gets 21 points, the dealer gets 20~17 points
The player gets 20 points, the dealer gets 19~17 points
The player gets 19 points, the dealer gets 18 and 17 points
The player gets 18 points and the dealer gets 17 points
The player starts to draw cards from 12 points and gets 18 points, which is equivalent to starting from H2 and gets H8, so the probability is G(H8), and the probability of the dealer getting 17 points is G(17). The probability of case 4 according to this is:
P4 = G(H8) × G(17)
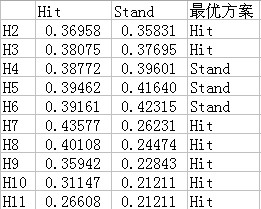
Similarly, P3, P2, and P1 can be calculated. Therefore, when the player's hand sum is H12 and the dealer's first card is 2, the winning probability of the player choosing Hit is:
P(H) = P1 + P21 + P22 + P23 + P24 = 0.36958
Calculated before, the probability of choosing Stand to win in this case P(S) = F(H2) = 0.35831
P(H) > P(S), so Hit is the optimal strategy.
In the same way, we can calculate the probability that the player chooses Hit to win when the player's hand is H12 and the dealer's first card is H3~H11. Counting all the cases, you get the following table:
Change the stakes and turn the tables
As mentioned earlier, even if you memorize these three matrices, the winning rate still cannot exceed half. The best strategy will only keep you from losing so fast, but it won't help you win. In 1963, Professor Edward Thorpe of the Massachusetts Institute of Technology conducted an experiment and found that the more small cards (7 and below) in the remaining cards, the easier it was for the dealer to win, and the remaining high cards (9, 10, J, Q) , K, A), the easier it is for the player to win. This is actually easy to understand. The dealer will keep drawing cards when the card is opened until the point is greater than or equal to 17. If there are more high cards in the remaining cards at this time, the possibility of the dealer busting will be greater. And when there are many big names, it is easier for players to adopt the Double strategy to increase profits.
At this point, you may have guessed that, if you want to win, you have to change your bets. Bet big when it's good and bet little when it's bad. But the question is, how do you know when the remaining cards are high? The answer is - sign up.
There is a basic card-keeping method called the Hi-Lo method. Its strategy is to make 2~6 as -1 point, 7~9 as 0 point, 10, J, Q, K, A as 1 point, and put all the cards that have been played. The scores of the cards are added up, and if the score is high, it means that there are fewer big cards in the remaining cards. However, the meanings of 15 points accumulated after 1 deck of cards are dealt and 15 points accumulated after 3 decks of cards are dealt are obviously different, so there is the following adjustment formula:

For example, there are 6 decks at the beginning of the game, and after 3 decks are dealt, 15 points are accumulated, then the real value is 15/3 = 5.
The book "Lost Genius" once introduced the story of a group of MIT top students in the 1990s who made 3 million madly through blackjack. This group of people is using the hi-lo method to keep cards. Although this method ignores the difference between 2 and 6, it is not perfect, but it is at least not easy to go wrong, knowing that it is better to win less than to lose.
In actual operation, the MIT team will scatter several scouts to record cards on different tables. Once a table is found to be very hot, it will send a signal to the partner to make a big bet, and the scout will continue to keep quiet. bet. The teamwork mode makes it easier to win big, and at the same time, it is also difficult to arouse the suspicion of the casino. The movie "Blackjack" tells such a story.
